KHTN - PreTS10 - 2025
[KHTN - PreTS10 - 2025] Bài 1: BIG3
Nộp bàiPoint: 25
Cho mảng ~A~ gồm ~N~ số nguyên ~A_1, A_2, ..., A_n~. Gọi mảng ~B~ là mảng được tạo bằng cách sắp xếp mảng ~A~ theo thứ tự giảm dần, tức là ~B_1 \ge B_2 \ge ... \ge B_n~. Hãy xác định giá trị phần tử ~B_3~.
INPUT
Dòng đầu tiên ghi số nguyên dương ~N~ (~3 ≤ N ≤ 10^7~).
Dòng thứ hai gồm ~N~ số nguyên dương ~A_1, A_2, ..., A_n~ (~A_i ≤ 10^9~).
OUTPUT
In ra một số nguyên duy nhất là kết quả của bài toán.
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~50~ | ~N \le 10^5~ |
| ~2~ | ~50~ | Không có ràng buộc gì thêm. |
SAMPLE INPUT
5
1 2 3 3 5
SAMPLE OUTPUT
3
[KHTN - PreTS10 - 2025] Bài 2: EQUA3
Nộp bàiPoint: 25
Cho phương trình bậc ba có dạng ~f(x) = ax^3 + bx^2 + cx + d~ trong đó a, b, c, d là các số nguyên dương.
Ta định nghĩa một "nghiệm" của phương trình là một số thực ~y~ sao cho: ~|f(y)| \le 10^{-9}~.
Hãy in ra một "nghiệm" bất kỳ của phương trình theo định nghĩa trên.
INPUT
Một dòng gồm 4 số nguyên dương ~a, b, c, d~ (~1 \le a, b, c, d \le 1000~) là các hệ số của phương trình.
OUTPUT
Một số thực duy nhất là kết quả của bài toán.
Có thể in ra số thực này theo độ chính xác bất kỳ, miễn thỏa điều kiện bài toán.
SAMPLE INPUT
1 6 11 6
SAMPLE OUTPUT
-1
Giải thích: phương trình ~x^3 + 6x^2 + 11x + 6 = (x + 1)(x + 2)(x + 3)~ có 3 nghiệm ~-1; -2; -3~.
[KHTN - PreTS10 - 2025] Bài 3: REC3
Nộp bàiPoint: 25
Cho một bảng hình chữ nhật gồm ~N~ hàng và ~M~ cột được tạo bởi ~N \times M~ ô vuông đơn vị. Có ~K~ ô trong bảng đã được đánh dấu. Một hình chữ nhật con là một tập hợp các ô vuông đơn vị tạo thành hình chữ nhật nằm hoàn toàn bên trong bảng. Hãy đếm số hình chữ nhật con chứa ít nhất một ô bị đánh dấu.
INPUT
- Dòng đầu tiên ghi 3 số nguyên dương ~N, M, K~ (~1 \le N, M \le 10^9; 1 \le K \le 20~)
- Trong ~K~ dòng sau, dòng thứ ~i~ gồm 2 số nguyên dương ~X_i, Y_i~ (~1 \le X_i \le N; 1 \le Y_i \le M~) là tọa độ của ô vuông thứ ~i~ bị đánh dấu.
OUTPUT
Một số nguyên duy nhất là kết quả của bài toán. Vì kết quả có thể rất lớn, hãy in ra kết quả modulo ~10^9+7~
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~25~ | ~K = 1~ |
| ~2~ | ~25~ | ~K = 2~ |
| ~3~ | ~50~ | Không có ràng buộc gì thêm. |
SAMPLE INPUT
2 3 1
1 1
SAMPLE OUTPUT
6
Giải thích: Có 6 hình chữ nhật con chứa ô vuông (~1, 1~).
[KHTN - PreTS10 - 2025] Bài 4: TITLE3
Nộp bàiPoint: 25
Cho một bảng hình chữ nhật gồm ~N~ hàng và ~M~ cột được tạo bởi ~N \times M~ ô vuông đơn vị. Có ~K~ ô trong bảng đã được đánh dấu. Hãy đếm số cách lát kín những ô không bị đánh dấu bằng những viên gạch hình chữ nhật kích cỡ ~1 \times 2~ hoặc ~2 \times 1~ sao cho mỗi viên gạch phải nằm hoàn toàn trong bảng và không có 2 viên gạch nào chồng lên nhau. Không được đặt viên gạch lên ô bị đánh dấu.
INPUT
- Dòng đầu tiên ghi 3 số nguyên dương ~N, M, K~ (~1 \le N \le 10, 1 \le M \le 1000, 0 \le K \le N \times M~)
- Trong ~K~ dòng sau, dòng thứ ~i~ gồm 2 số nguyên dương ~X_i, Y_i~ (~1 \le X_i \le N; 1 \le Y_i \le M~) là tọa độ của ô vuông thứ ~i~ bị đánh dấu.
OUTPUT
Một số nguyên duy nhất là kết quả của bài toán. Vì kết quả có thể rất lớn, hãy in ra kết quả modulo ~10^9+7~
SUBTASKS
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~25~ | ~N \le 2~ |
| ~2~ | ~25~ | ~N = 3, K = 0.~ |
| ~3~ | ~50~ | Không có ràng buộc gì thêm. |
SAMPLE INPUT
2 4 2
1 4
2 2
SAMPLE OUTPUT
1
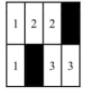
Giải thích: Ta lát như hình dưới đây (những ô màu đen là bị đánh dấu, 2 ô có cùng số thuộc cùng 1 viên gạch).