[WS x ClueOJ] Contest Giải phóng miền Nam, thống nhất đất nước
WSC1: Không làm được là gay
Nộp bàiPoint: 10
Trên một bảng A kích thước ~n \times n~ với ~n~ là số lẻ, các ô trên bảng có thể chứa một trong ba ký tự: g, a,y.
Chúng ta định nghĩa các ô thuộc tập ~Y~ bao gồm các ô nằm trên:
- Đường chéo bắt đầu từ ô trên cùng bên trái và kết thúc tại ô trung tâm của bảng.
- Đường chéo bắt đầu từ ô trên cùng bên phải và kết thúc tại ô trung tâm của bảng.
- Đường thẳng đứng bắt đầu từ ô trung tâm,kéo thẳng xuống và kết thúc tại biên dưới của bảng.
Một bảng tồn tại ~Y-letter~ nếu và chỉ nếu:
- Các ô thuộc tập ~Y~ có cùng một ký tự.
- Các ô không thuộc tập ~Y~ có cùng một ký tự.
- Các ô thuộc tập ~Y~ và các ô không thuộc tập ~Y~ phải có ký tự khác nhau.
Bạn có một thao tác duy nhất là thay đổi ký tự của một ô thành một trong ba ký tự g, a, hoặc y.
Hãy xác định số thao tác ít nhất cần thực hiện để bảng có thể xuất hiện ~Y-letter~.
Input
Dòng đầu tiên là số nguyên ~n~ ~(1 \le n \le 10^3)~
~n~ dòng tiếp theo,mỗi dòng gồm ~n~ kí tự ~s_i~ ~(s_i \in \{'g','a','y'\})~
Output
Một dòng duy nhất là số thao tác ít nhất
Subtask
- Subtask 1 : Không có ràng buộc gì.
Sample Input
3
ayy
aag
gag
Sample Output
3
Giải thích

Ô tô màu xanh là những ô bị thay đổi
WSC1: Hại điện
Nộp bàiPoint: 20
Trong ngôi nhà thông minh của ~Zinno~, ~n~ con robot được kết nối với nhau theo một mạng lưới tuần tự. Mỗi robot trong danh sách được kết nối trực tiếp với robot đứng trước và robot đứng sau nó (trừ robot đầu tiên và cuối cùng).
Để thực hiện một tác vụ cụ thể, ~Zinno~ cần kích hoạt một nhóm robot hoạt động đồng thời. Do đặc thù của mạng lưới kết nối, tín hiệu điều khiển phải được truyền theo chuỗi từ một robot đầu tiên trong nhóm đến các robot kế cận. Việc kích hoạt các robot không liên tiếp sẽ phức tạp hơn, đòi hỏi gửi nhiều tín hiệu riêng lẻ, gây tốn kém năng lượng và tăng độ trễ.
Mỗi con robot yêu cầu một lượng sạc ban đầu là ~c_i~ để có thể hoạt động. Sau khi được sạc, khi hoạt động liên tục, mỗi robot tiêu thụ một lượng điện năng là ~p_i~ mỗi đơn vị thời gian. Do yêu cầu về tính đồng bộ và hiệu quả của hệ thống điều khiển tuần tự, ~Zinno~ chỉ xem xét việc sử dụng các đoạn robot liên tiếp trong danh sách cho mỗi tác vụ.
Khi sử dụng một đoạn các con robot liên tiếp từ vị trí ~u~ đến vị trí ~v~ trong danh sách, tổng chi phí năng lượng cho tác vụ đó được tính như sau:
$$ max(c_u,c_{u+1},...,c_v)+(v-u+1)\times \sum_{i=u}^{v}p_i $$
Input
Dòng đầu tiên là số nguyên dương ~n~ và ~k~ ~(1 \le n \le 10^5, 1 \le k \le 10^{15})~
Dòng thứ hai là ~n~ số nguyên dương ~c_i~ ~(1 \le c_i \le 10^5)~
Dòng thứ ba là ~n~ số nguyên dương ~p_i~ ~(1 \le p_i \le 10^5)~
Output
Một dòng duy nhất là số robot tối đa mà ~Zinno~ có thể dùng mà tổng chi phí không quá ~k~
Subtask
- Subtask 1 : ~30\%~ số điểm có ~n \le 10^3~
- Subtask 2 : ~70\%~ số điểm còn lại Không có ràng buộc gì thêm.
Sample Input
5 25
3 6 1 3 4
2 1 3 4 5
Sample Output
3
WSC1: Chọn bạn mà chơi
Nộp bàiPoint: 30
Cô giáo ~Nana~ luôn trăn trở về việc xây dựng một tập thể lớp không chỉ giỏi giang mà còn gắn bó và yêu thương nhau. Trong lớp của cô, tồn tại những nhóm bạn thân thiết, nhưng cũng có những học sinh còn e dè, ít giao tiếp với những bạn khác. Với mong muốn tạo cơ hội cho tất cả các em được kết bạn và làm việc cùng nhau, cô ~Nana~ quyết định tổ chức các trò chơi nhóm đặc biệt.
Để đảm bảo tính công bằng và khuyến khích sự giao lưu, cô ~Nana~ đặt ra một số nguyên tắc chia nhóm mà các em phải tuân theo:
- Mỗi học sinh chỉ thuộc về một nhóm duy nhất. Không ai được đồng thời tham gia nhiều nhóm.
- Những đôi bạn thân không được ở cùng một nhóm. Cô muốn các em mở rộng vòng bạn bè của mình.
Ban đầu, cô ~Nana~ lo lắng việc chia nhóm ngẫu nhiên có thể gây khó khăn trong việc tạo sự kết nối. Sau khi suy nghĩ, cô nhận thấy rằng việc xếp những đôi bạn thân vào hai nhóm liền kề sẽ tạo ra những "cầu nối" tự nhiên giữa các nhóm. Các em vốn đã có sự gắn kết, nên khi ở hai nhóm gần nhau, các em sẽ dễ dàng trò chuyện, hỗ trợ và khuyến khích các bạn trong nhóm mình giao lưu với bạn thân của mình ở nhóm kế bên. Điều này sẽ giúp phá vỡ các rào cản, thúc đẩy sự hòa nhập và lan tỏa tinh thần đồng đội trong lớp.
Do đó, cô ~Nana~ quyết định thêm một quy tắc quan trọng:
- Những đôi bạn thân sẽ phải thuộc ~2~ nhóm liên tiếp,hay nó cách khác nếu ~u~ và ~v~ là một cặp chơi thân, ~u~ ở nhóm ~x~, và ~v~ ở nhóm ~y~ ~(y\neq x)~ sao cho ~|x-y|=1~
Bạn hãy giúp cô giáo ~Nana~ xác định số lượng nhóm tối đa mà cô có thể chia lớp theo các quy tắc đã đề ra. Nếu không có cách nào để chia lớp theo đúng các quy tắc này, hãy in ra thông báo IMPOSSIBLE.
Input
Dòng đầu tiên là số nguyên ~n~ ~(1 \le n \le 500)~ ~-~ số lượng học sinh trong lớp, và ~m~ ~(1 \le m \le 10^4)~ ~-~ số lượng cặp chơi thân.
~m~ dòng tiếp theo là ~2~ số ~u~ và ~v~ ~(1 \le u,v \le n, u \neq v)~- thể hiện ~u,v~ là một cặp chơi thân với nhau.
Output
In ra một số duy nhất là lượng nhóm tối đa có thể chia được, nếu không thể chia lớp theo các quy tắc,in ra IMPOSSIBLE
Subtask
- Subtask 1 : ~10\%~ số điểm có ~m=n-1~, dòng thứ ~i~ có ~u_i=i,v_i=i+1~ ~\forall i = 1,2,3,...n-1~
- Subtask 2 : ~20\%~ số điểm có đồ thị đã cho là đồ thị cây
- Subtask 3 : ~70\%~ số điểm còn lại Không có ràng buộc gì thêm.
Sample Input
6 6
3 4
4 5
1 2
2 4
4 6
1 3
Sample Output
4
Giải thích:
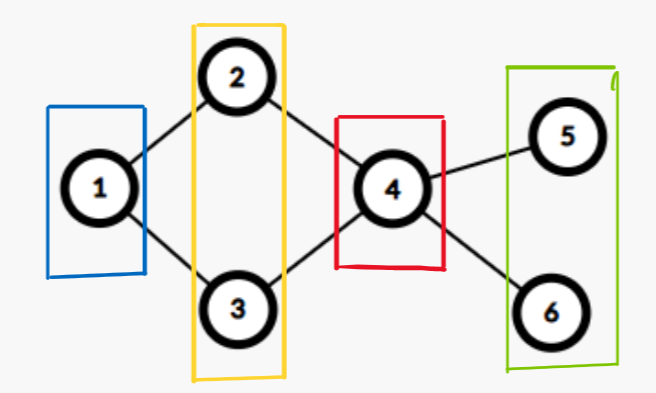
WSC1: Tối Ưu Mạng Địa Đạo
Nộp bàiPoint: 40
"Giữa lòng cuộc chiến tranh khốc liệt, nơi bom đạn và gian khổ không ngừng thử thách ý chí con người, tinh thần quật cường và trí tuệ sáng tạo của quân và dân Việt Nam, đặc biệt là các chiến sĩ du kích, đã tỏa sáng rực rỡ. Một trong những biểu tượng tiêu biểu cho sự kiên cường và bí mật chiến đấu là hệ thống địa đạo Củ Chi, những "con đường thép" ẩn mình sâu dưới lòng đất. Đây không chỉ là nơi trú ẩn an toàn trước hỏa lực dày đặc của kẻ thù, mà còn là mạng lưới giao thông, liên lạc bí mật, kết nối các căn cứ địa và chiến lược, giúp vận chuyển lực lượng, vũ khí và mệnh lệnh một cách kín đáo. Địa đạo Củ Chi, cùng với các chiến công khác, góp phần quan trọng vào thành công của những chiến dịch lớn, đặc biệt là Chiến dịch Hồ Chí Minh năm 1975, dẫn đến thắng lợi vĩ đại vào ngày 30/4, giải phóng miền Nam, thống nhất đất nước."
Trong những ngày tháng hào hùng của chiến dịch Hồ Chí Minh, hệ thống địa đạo đóng vai trò huyết mạch trong việc đảm bảo liên lạc thông suốt và bí mật giữa các đơn vị cách mạng. Hãy hình dung mạng lưới địa đạo như một đồ thị cây ~G~ khổng lồ, bao gồm ~N~ hầm chỉ huy then chốt (các đỉnh của đồ thị), đóng vai trò là trung tâm điều phối thông tin, và ~N-1~ đoạn địa đạo kết nối trực tiếp giữa các hầm này (tương ứng với các cạnh của đồ thị). Cấu trúc cây đảm bảo rằng luôn tồn tại một tuyến liên lạc duy nhất và không bị trùng lặp giữa hai hầm chỉ huy bất kỳ, yếu tố sống còn để tránh bị lộ thông tin và đảm bảo mệnh lệnh được truyền đạt chính xác.
Trong mô hình này, mỗi đoạn địa đạo nối hai hầm chỉ huy ~u~ và ~v~ có một thuộc tính quan trọng, thể hiện "Độ rõ Tín hiệu Liên lạc" ~(D)~. Ban đầu, do điều kiện xây dựng khác nhau, chiều dài, độ sâu, và các biện pháp bảo vệ khác nhau, độ rõ tín hiệu này có thể không đồng đều giữa các đoạn địa đạo. Độ rõ tín hiệu càng thấp đồng nghĩa với việc thông tin truyền đi càng khó khăn, dễ bị nhiễu hoặc mất mát, ảnh hưởng đến sự phối hợp tác chiến.
Bộ Chỉ huy nhận được ~Q~ yêu cầu "Kiểm tra Đường dây Nóng", mỗi yêu cầu là một cặp hầm chỉ huy ~(u, v)~.
Nhiệm vụ:
Xác định số biện pháp kỹ thuật tối thiểu cần thực hiện trên đường đi duy nhất từ hầm ~u~ đến hầm ~v~ để Chuẩn hóa Độ rõ Tín hiệu trên tuyến liên lạc này.
Chuẩn hóa Độ rõ Tín hiệu trên tuyến liên lạc nghĩa là điều chỉnh độ rõ tín hiệu của một số đoạn địa đạo trên tuyến sao cho tất cả các đoạn đều có cùng một giá trị độ rõ tín hiệu.
Mỗi biện pháp kỹ thuật là việc chọn một đoạn địa đạo trên tuyến và thay đổi độ rõ tín hiệu của nó thành bất kỳ mức nào mong muốn.
Lưu ý rằng: Sau mỗi nhiệm vụ, trạng thái mạng địa đạo trở về ban đầu, bởi vì trong thực tế, các phương án cải thiện tín hiệu chỉ được lên kế hoạch và giả lập, chưa thực hiện ngay lập tức để bảo mật và đảm bảo an toàn cho toàn chiến dịch.
Hãy lập trình để tìm ra con số tối thiểu này cho mỗi truy vấn, thể hiện khả năng đảm bảo thông tin liên lạc thông suốt và hiệu quả, góp phần vào thắng lợi cuối cùng của chiến dịch Hồ Chí Minh trong địa đạo mô phỏng này.
Input Format
- Dòng đầu tiên: Một số nguyên ~N~ ~(1 \le N \le 10^5 )~ — số lượng hầm chỉ huy.
- ~N-1~ dòng tiếp theo: Mỗi dòng gồm 3 số nguyên ~u~, ~v~, ~D~ ~(1 \le u,v \le n , u \neq v , D \le 26)~ — mô tả đoạn địa đạo nối ~u~ và ~v~ với độ rõ tín hiệu ~D~.
- Dòng tiếp theo: Một số nguyên ~Q~ ~(1 \le Q \le 10^5)~ — số lượng yêu cầu kiểm tra.
- ~Q~ dòng tiếp theo: Mỗi dòng gồm hai số nguyên ~u~, ~v~ — yêu cầu kiểm tra tuyến liên lạc từ ~u~ đến ~v~.
Output Format
- Gồm ~Q~ dòng, mỗi dòng là số biện pháp kỹ thuật tối thiểu cần thực hiện cho yêu cầu tương ứng.
Subtask
- Subtask 1: Có ~20\%~ số điểm có ~1 \leq N, Q \leq 500~
- Subtask 2: ~30\%~ số điểm có ~1 \leq N, Q \leq 5 \times 10^3~
- Subtask 3: ~50\%~ số điểm còn lại không có giới hạn gì thêm
Sample Input
8
1 2 6
1 3 4
3 6 6
3 8 8
8 7 2
2 5 3
2 4 6
4
4 6
8 4
6 5
7 4
Sample Output
1
2
2
3
Giải thích
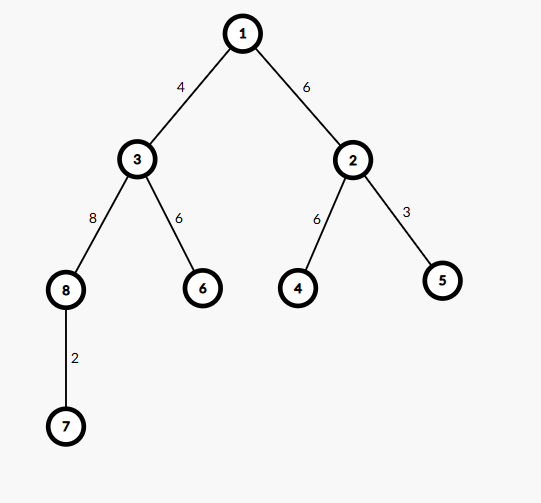
Ở truy vấn đầu tiên, ta thay đổi trọng số của cạnh ~[1,3]~ thành ~6~. Sau thao tác này, tất cả các cạnh trên đường đi từ ~4~ đến ~6~ đều có trọng số bằng ~6~. Do đó, đáp án là ~1~.
Ở truy vấn thứ hai, ta thay đổi trọng số của các cạnh ~[8,3]~ và ~[3,1]~ thành ~6~. Sau các thao tác này, tất cả các cạnh trên đường đi từ ~8~ đến ~4~ đều có trọng số bằng ~6~. Do đó, đáp án là ~2~.
Ở truy vấn thứ ba, ta thay đổi trọng số của các cạnh ~[1,3]~ và ~[5,2]~ thành ~6~. Sau các thao tác này, tất cả các cạnh trên đường đi từ ~6~ đến ~5~ đều có trọng số bằng ~6~. Do đó, đáp án là ~2~.
Ở truy vấn thứ tư, ta thay đổi trọng số của các cạnh ~[8,7]~, ~[8,3]~ và ~[1,3]~ thành ~6~. Sau các thao tác này, tất cả các cạnh trên đường đi từ ~7~ đến ~4~ đều có trọng số bằng ~6~. Do đó, đáp án là ~3~.
WSC1: Khảo sát sóng âm
Nộp bàiPoint: 50
Trong một buổi hòa nhạc, âm thanh từ một nhạc cụ cụ thể được ghi lại và biểu diễn dưới dạng một chuỗi các mẫu số liệu, bao gồm ~n~ thời điểm. Tại mỗi thời điểm ~i~, chúng ta có một giá trị ~A_i~ , được gọi là cường độ âm tại thời điểm đó. Mỗi ~A_i~ tương ứng với biên độ dao động của sóng âm tại thời điểm ~i~. Để phân tích sự phức tạp và đa dạng của âm thanh này, các nhà nghiên cứu âm học đã đưa ra khái niệm "độ biến thiên âm".
Độ biến thiên âm giữa hai thời điểm ~i~ và ~j~ (với ~i \le j~) được định nghĩa là số lượng các mức cường độ âm khác nhau xuất hiện trong khoảng thời gian từ thời điểm ~i~ đến thời điểm ~j~ (bao gồm cả thời điểm ~i~ và ~j~). Chúng ta gọi số này là hàm ~f(i,j)~.
Ví dụ, nếu chuỗi cường độ âm từ thời điểm ~i~ đến ~j~ là ~[1,2,1,3]~, thì các mức cường độ âm khác nhau xuất hiện là ~1,2,3~. Do đó, độ biến thiên âm ~f(i,j)=3~.
Để đánh giá tổng thể sự biến đổi của âm thanh trong suốt buổi hòa nhạc, các nhà nghiên cứu muốn tính toán tổng bình phương của tất cả các độ biến thiên âm có thể có. Tổng này được gọi là "chỉ số biến thiên âm", kí hiệu ~\Delta f~.Nó được xác định bằng cách xét tất cả các cặp thời điểm ~(x,y~) sao cho ~(1 \le x \le y \le n)~, tính độ biến thiên âm ~f(x,y)~ cho mỗi cặp, lấy bình phương của nó, và sau đó cộng tất cả các bình phương này lại
Hay nói cách khác, ~\Delta f~ được tính như sau: $$ \Large \Delta f=\sum_{x=1}^{n} \sum_{y=x}^{n} f(x,y)^2 $$
Hãy tính ~\Delta f~ giúp các nhà nghiên cứu âm học nhé
Vì ~\Delta f~ có thể rất lớn nên hãy lấy dư với ~10^9+7~.
Input
Dòng đầu tiên là số nguyên ~n~ ~(1 \le n \le 10^5)~
Dòng tiếp theo là ~n~ số nguyên ~A_i~ ~(1 \le A_i \le 10^5, \forall i \in [1,n])~
Output
Một dòng duy nhất là ~\Delta f~ chia dư cho ~10^9+7~
Subtask
- Subtask 1 : ~20\%~ số điểm có ~A_i \neq A_j~ ~\forall~ ~i,j \in [1,n]~ , ~i \neq j~
- Subtask 2: ~30\%~ số điểm có ~n \le 10^3~
- Subtask 3: ~50\%~ số điểm còn lại không có giới hạn gì thêm
Sample Input
3
1 2 3
Sample Output
20
Giải thích
~f(1,1)~ ~=1^2~
~f(1,2)~ ~=~ ~2^2~
~f(1,3)~ ~=~ ~3^2~
~f(2,2)~ ~=~ ~1^2~
~f(2,3)~ ~=~ ~2^2~
~f(3,3)~ ~=~ ~1^2~
~\Longrightarrow~ ~S=1^2 + 2^2 + 3^2+ 1^2 + 2^2 + 1^2=20~
WS1: Tàu lửa meLona
Nộp bàiPoint: 60
Thành phố hiện đại meLona, nơi Sơn sinh sống, được quy hoạch thành một mạng lưới giao thông dạng lưới vuông góc. Thành phố có kích thước ~W \times H~, với ~W~ tuyến đường dọc từ Bắc xuống Nam (đánh số từ ~1~ đến ~W~, từ Tây sang Đông), và ~H~ tuyến đường ngang từ Đông sang Tây (đánh số từ ~1~ đến ~H~, từ Bắc xuống Nam). Giao điểm giữa một đường dọc và một đường ngang được gọi là nút giao thông, ký hiệu là ~(u, v)~.
Hệ thống vận tải công cộng ở meLona bao gồm các tàu lửa tự động, chạy liên tục quanh các khu vực dân cư theo các tuyến đường hình chữ nhật, theo chiều kim đồng hồ. Mỗi tàu chạy không ngừng theo chu kỳ trên một chu vi hình chữ nhật cố định.
Có tổng cộng ~N~ tuyến tàu lửa như vậy. Tuyến thứ ~i~ chạy quanh hình chữ nhật có góc trên bên trái là ~(X_{1i}, Y_{1i})~ và góc dưới bên phải là ~(X_{2i}, Y_{2i})~. Vào thời điểm ~0~, tàu ~i~ đã bắt đầu hành trình từ đỉnh ~(X_{1i}, Y_{1i})~ và đã chạy được ~T_i~ đơn vị thời gian.
Sơn cần đi từ nhà ở vị trí ~(X_S, Y_S)~ đến trường tại vị trí ~(X_T, Y_T)~. Sơn chỉ được phép di chuyển bằng tàu lửa và có thể lên hoặc xuống tàu tại bất kỳ thời điểm nào tàu đi qua nút mà Sơn đang đứng. Tuy nhiên, sau khi xuống một tàu tại thời điểm ~t~, Sơn chỉ có thể lên một tàu khác bắt đầu từ thời điểm ~t + 1~ trở đi.
Hãy tính thời gian nhanh nhất để Sơn có thể đến được trường.
Input
Dòng đầu tiên chứa sáu số nguyên ~W, H, X_S, Y_S, X_T, Y_T~ ~(1 \leq X_S, X_T \leq W \leq 1000,\ 1 \leq Y_S, Y_T \leq H \leq 1000)~.
Dòng thứ hai chứa số nguyên dương ~N~ ~(1 \leq N \leq 1000)~ ~-~số tuyến tàu lửa.
~N~ dòng tiếp theo, dòng thứ ~i~ chứa ~5~ số nguyên: ~X_{1i}, Y_{1i}, X_{2i}, Y_{2i}, T_i~, mô tả hành trình tàu ~i~.
Các điều kiện đảm bảo: ~1 \leq X_{1i}, X_{2i} \leq W~ , ~1 \leq Y_{1i}, Y_{2i} \leq H~ ~0 \leq T_i < 2 \times (|X_{2i} - X_{1i}| + |Y_{2i} - Y_{1i}|)~
Output
In ra một số nguyên duy nhất là thời gian sớm nhất Sơn có thể đến trường.
Subtask
Subtask ~1~ (~25\%~ số điểm): ~1 \leq W, H, N \leq 30~.
Subtask ~2~ (~25\%~ số điểm): ~1 \leq W, H, N \leq 300~.
Subtask ~3~ (~25\%~ số điểm): ~1 \leq W, H, N \leq 500~.
Subtask ~4~ (~25\%~ số điểm): không có ràng buộc nào thêm.
Sample Input
10 10 1 3 10 1
3
1 3 5 6 4
5 5 7 10 1
7 1 10 5 9
Sample Output
50