Cô giáo ~Nana~ luôn trăn trở về việc xây dựng một tập thể lớp không chỉ giỏi giang mà còn gắn bó và yêu thương nhau. Trong lớp của cô, tồn tại những nhóm bạn thân thiết, nhưng cũng có những học sinh còn e dè, ít giao tiếp với những bạn khác. Với mong muốn tạo cơ hội cho tất cả các em được kết bạn và làm việc cùng nhau, cô ~Nana~ quyết định tổ chức các trò chơi nhóm đặc biệt.

Để đảm bảo tính công bằng và khuyến khích sự giao lưu, cô ~Nana~ đặt ra một số nguyên tắc chia nhóm mà các em phải tuân theo:

1. Mỗi học sinh chỉ thuộc về một nhóm duy nhất. Không ai được đồng thời tham gia nhiều nhóm.
2. Những đôi bạn thân không được ở cùng một nhóm. Cô muốn các em mở rộng vòng bạn bè của mình.

Ban đầu, cô ~Nana~ lo lắng việc chia nhóm ngẫu nhiên có thể gây khó khăn trong việc tạo sự kết nối. Sau khi suy nghĩ, cô nhận thấy rằng việc xếp những đôi bạn thân vào hai nhóm liền kề sẽ tạo ra những "cầu nối" tự nhiên giữa các nhóm. Các em vốn đã có sự gắn kết, nên khi ở hai nhóm gần nhau, các em sẽ dễ dàng trò chuyện, hỗ trợ và khuyến khích các bạn trong nhóm mình giao lưu với bạn thân của mình ở nhóm kế bên. Điều này sẽ giúp phá vỡ các rào cản, thúc đẩy sự hòa nhập và lan tỏa tinh thần đồng đội trong lớp.

Do đó, cô ~Nana~ quyết định thêm một quy tắc quan trọng:

• Những đôi bạn thân sẽ phải thuộc ~2~ nhóm liên tiếp,hay nó cách khác nếu ~u~ và ~v~ là một cặp chơi thân, ~u~ ở nhóm ~x~, và ~v~ ở nhóm ~y~ ~(y\neq x)~ sao cho ~|x-y|=1~

Bạn hãy giúp cô giáo ~Nana~ xác định số lượng nhóm tối đa mà cô có thể chia lớp theo các quy tắc đã đề ra. Nếu không có cách nào để chia lớp theo đúng các quy tắc này, hãy in ra thông báo IMPOSSIBLE.

Input

Dòng đầu tiên là số nguyên ~n~ ~(1 \le n \le 500)~ ~-~ số lượng học sinh trong lớp, và ~m~ ~(1 \le m \le 10^4)~ ~-~ số lượng cặp chơi thân.

~m~ dòng tiếp theo là ~2~ số ~u~ và ~v~ ~(1 \le u,v \le n, u \neq v)~- thể hiện ~u,v~ là một cặp chơi thân với nhau.

Output

In ra một số duy nhất là lượng nhóm tối đa có thể chia được, nếu không thể chia lớp theo các quy tắc,in ra IMPOSSIBLE

Subtask

• Subtask 1 : ~10\%~ số điểm có ~m=n-1~, dòng thứ ~i~ có ~u_i=i,v_i=i+1~ ~\forall i = 1,2,3,...n-1~
• Subtask 2 : ~20\%~ số điểm có đồ thị đã cho là đồ thị cây
• Subtask 3 : ~70\%~ số điểm còn lại Không có ràng buộc gì thêm.

Sample Input

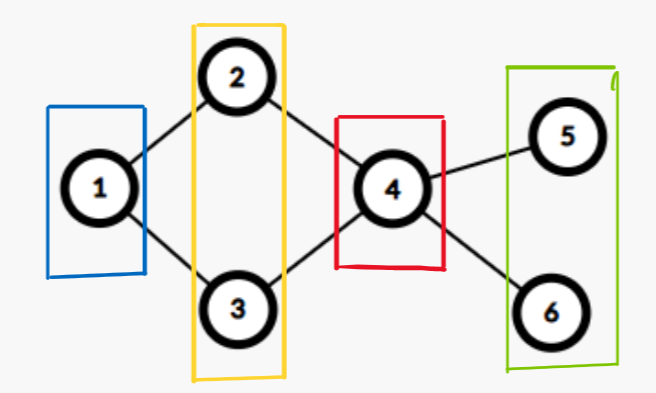
6 6
3 4
4 5
1 2
2 4
4 6
1 3 

Sample Output

4

Giải thích: