Tóm tắt đề bài như sau:

Nhiệm vụ của chúng ta là chia các đỉnh này thành số lượng nhóm được đánh số lớn nhất có thể ~(1, 2, 3, ...)~ sao cho:

Mỗi đỉnh thuộc chính xác một nhóm.

Nếu có một cạnh ~[u, v]~, và ~u~ thuộc nhóm số ~x~, thì ~v~ phải thuộc nhóm ~x - 1~ hoặc ~x + 1~

Sub 1: Đồ thị là đồ 1 đường thẳng

Đơn giản câu trả lời là ~n~ nhóm

Sub 2: Đồ thị đã cho là đồ thị cây

Một quan sát quan trọng ở đây là: số lượng nhóm tối đa trong một đồ thị cây chính khoảng cách xa nhất giữa các cặp đỉnh trong cây tính theo số nút,hay chính là đường kính của cây tính theo số nút

Sub 3:

Một chi tiết quan trọng là đồ thị được cho không phải lúc nào cũng liên thông

Nhưng trước tiên hãy làm việc với đồ thị liên thông đã

Ta thấy việc gán nhóm trên có thể không thực hiện được trong một số trường hợp như sau:

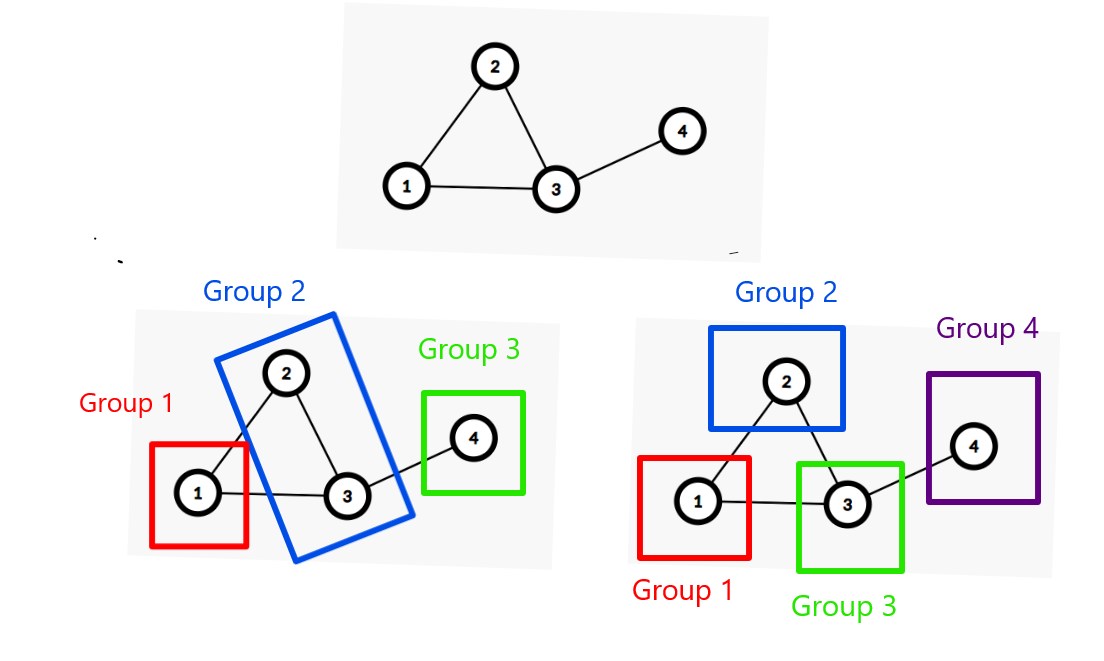
Ta thấy ~2~ cách xếp nhóm trên đều không hoạt động

Vậy tại sao điều này không hoạt động?

Ta có thể thấy

Một tam giác ~(A-B-C-A)~ sẽ dẫn đến việc gán nhóm bị xung đột: ~A = 1 → B = 2 → C = 3 → A = 4~, nhưng ~A~ và ~C~ liền kề nhau, nên phải thỏa mãn điều kiện ~|4 - 3| = 1~ ~→~ mâu thuẫn.

Hay nói một cách khác nếu đồ thị chứa một chu trình có độ dài lẻ thì không thể gán nhóm một cách hợp lệ.

Một nhận xét quan trọng khác là:

Nếu một thành phần liên thông của đồ thị có thể được chia thành k nhóm ~(k>2)~ thỏa mãn các điều kiện, thì nó cũng có thể được chia thành ~2~ nhóm.

Một cách trực quan,nếu chúng ta có một cách chia thành ~k>2~ nhóm, ta có thể "gộp" các nhóm có số thứ tự cùng tính chẵn lẻ lại với nhau. Ví dụ, nhóm ~1, 3, 5,...~ vào một tập và nhóm ~2, 4, 6,...~ vào một tập. Vì các cạnh chỉ có thể nối giữa các nhóm có số thứ tự liên tiếp, nên sẽ không có cạnh nào nối giữa các đỉnh trong cùng một tập mới này. Do đó, cách chia thành ~2~ nhóm vẫn hợp lệ.

Nói cách khác, chỉ cần kiểm tra xem đồ thị có phải là đồ thị hai phía hay không — tức là ta có thể chia các đỉnh thành ~2~ tập sao cho không có cạnh nào nối giữa các đỉnh trong cùng một tập là ta có thể biết chúng ta có thể chia thành các nhóm hợp lệ hay không

Trong trường hợp đồ thị không liên thông, chúng ta sẽ tính số lượng nhóm lớn nhất cho mỗi thành phần liên thông của đồ thị, sau đó cộng tổng các giá trị này lại.

Tóm lại, bài toán có thể rút gọn thành hai bước sau:

• Kiểm tra xem đồ thị có phải là ~2~ phía để xác định xem cách chia hợp lệ có tồn tại không.

• Với mỗi thành phần liên thông trong đồ thị, tìm số lượng nhóm lớn nhất có thể chia các đỉnh, và trả về tổng các giá trị đó.

Để kiểm tra xem đồ thị có phải là hai phía hay không, ta sẽ "tô màu" các đỉnh bằng hai màu khác nhau (mỗi màu đại diện cho một nhóm), đảm bảo rằng hai đỉnh được nối trực tiếp luôn có màu khác nhau.

Nếu quá trình tô màu bị thất bại ở đâu đó (tức có hai đỉnh liền kề cùng màu), thì đồ thị không phải là ~2~ phía,

Để tìm được số nhóm lớn nhất ~2~ ta làm gần giống như Sub 2.

Nếu ta cấu trúc lại đồ thị như một cây, với các đỉnh khác nhau đóng vai trò làm gốc.Thì số lượng nhóm tối đa chính là là đường đi ngắn nhất dài nhất giữa bất kỳ cặp đỉnh nào trong thành phần liên thông đó tính theo số nút

#include <bits/stdc++.h>
using namespace std;

int n, m;
vector<vector<int>> a;
vector<int> c;

bool check(int s) {
    queue<int> q;
    q.push(s);
    c[s] = 0;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int v : a[u]) {
            if (c[v] == c[u]) return false;
            if (c[v] == -1) {
                c[v] = 1 - c[u];
                q.push(v);
            }
        }
    }
    return true;
}

int depth(int s) {
    queue<int> q;
    vector<int> dist(n, -1);
    q.push(s);
    dist[s] = 0;
    int dep = 0;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int v : a[u]) {
            if (dist[v] == -1) {
                dist[v] = dist[u] + 1;
                dep = max(dep, dist[v]);
                q.push(v);
            }
        }
    }
    return dep + 1;
}

int sol() {
    c.assign(n, -1); 
    vector<bool> visited(n, false); 
    int ans = 0;

    for (int i = 0; i < n; i++) {
        if (c[i] != -1) continue;
        if (!check(i)) return -1;
        int dep = 0;
        queue<int> q;
        q.push(i);
        visited[i] = true;
        while (!q.empty()) {
            int u = q.front();
            q.pop();
            dep = max(dep, depth(u));
            for (int v : a[u]) {
                if (!visited[v]) {
                    visited[v] = true;
                    q.push(v);
                }
            }
        }
        ans += dep;
    }
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    a.resize(n);
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        a[u].push_back(v);
        a[v].push_back(u);
    }
    int ans = sol();
    if (ans == -1) cout << "IMPOSSIBLE\n";
    else cout << ans << '\n';

    return 0;
}